- Ruote da strada compatibili 25mm Largo,38 mm di profondità
-Mozzo leggero diritto Powerway con cuscinetto in ceramica
-Raggi Sapim-cx ray
| Modello:PL38C-PR36-CB | Marchio:Superstrada |
| Materiale della ruota:Carbonio T700 +30%T800 | Dimensione:700°C |
| Larghezza del cerchio:25 mm | Centro:Mozzo leggero diritto Powerway con cuscinetto in ceramica |
| Profondità del cerchio:38 mm | Raggi:Raggi Sapim a raggi C |
| Tipo di cerchio:Copertoncino Tubeless Letturay | Foro per i raggi:20-24H |
| Il peso:1450 +/- 30 g per tubeless da 38 mm | Capezzoli:Capezzolo in lega |
| Fine:Opaco/lucido | Pressione massima dei pneumatici:125 Psi/8,5 Bar |
| Tessere:Regno Unito,3K,12K | Peso massimo del ciclista:125 kg |
| Pista del freno:Carbonio, basalto, twill 3K | Tensione massima dei raggi:130 kgf |
| Corpo cassetta:Shimano/Campagnolo | Planarità della pista del freno:<0,15 mm |
| Compreso:Spiedo, nastro adesivo, raggio di ricambio | Rotondità:<0,25 mm |
| Decalcomania:Personalizzato | Standard:EN |
| Affare:OEM e ODM | Garanzia:2 anni |
| Spedizione:Sono disponibili DPD (tasse incluse). | Porta:Xiamen |
Descrizione del modello G3 700C 25 mm di larghezza 38 mm di carbonio leggero copertoncino Tybeless ReadyRuote Con Raggi Sapim
Set di ruote per copertoncino in carbonio completamente leggero da 25 mm di larghezza e 38 mm di profondità, pronto per tubeless. Offre stabilità al vento laterale e il design del cerchio TWC38C aerodinamicamente efficiente da superroad.
Mozzo in carbonio Powerway R36 con cuscinetto in ceramica nelle nostre ruote per bici da strada tubeless in carbonio leggero da 38 mm. Il motivo per cui preferiamo utilizzare il mozzo powerway con le nostre ruote, perché è più leggero del mozzo di altre marche,
La resistenza al rotolamento è la carta vincente promossa dalle ventole con cuscinetti in ceramica. Un cuscinetto in ceramica è anche più duro dei cuscinetti in acciaio, il che migliora la durata e inoltre non arrugginiscono, quindi dovrebbe essere necessaria una minore manutenzione.
Tecnologia della pista frenante in carbonio modellato, pista frenante alta TG 240 evita la deformazione per le discese più tecniche, Max Wider in 28 mm, resistenza al rotolamento ridotta per produrre la più leggera,
le ruote offrono un'incredibile stabilità dall'ampio profilo, cerchi più larghi per un migliore controllo e maneggevolezza di queste ruote..
Perché i cerchi da strada tubeless compatibili? Migliore resistenza al rotolamento rispetto al copertoncino standard, maggiore potenza per il ciclista. Il secondo, sarà ridotta la pressione dei pneumatici. Il terzo, più aerodinamico rispetto al copertoncino standard.
Perché scegliamo cerchi da strada larghi 28 mm a forma di U? Sarà ridotta la resistenza al rotolamento, come sappiamo, quando i cerchi sono leggermente più larghi del pneumatico quando viene a contatto con il suolo, fornirà un enorme vantaggio in termini di resistenza laterale,
otterrai un migliore controllo e maneggevolezza. Il risultato in una maggiore velocità e meno potenza da te stesso. Avrai anche un vantaggio aerodinamico.
Sono disponibili ruote per biciclette in carbonio OEM, se hai bisogno di altri mozzi, raggi e cerchi per ruote, non esitare a inviarci un messaggio.
Cosa stai misurando?
Puoi saltare questa sezione se lo desideri. Non è necessario conoscere la formula per la lunghezza dei raggi. Il software di calcolo della lunghezza dei raggi fa il numero per te.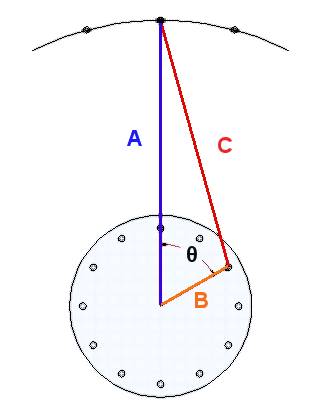
Ma nel caso la matematica ti interessi, ecco come viene calcolata la lunghezza dei raggi. È un problema di trigonometria, in due passaggi.
Il primo passo è calcolare la lunghezza del terzo lato di un triangolo secondo la formula della regola del coseno,
_________________
C u003d \/A2 + B2 - 2AB cos θ
dove
· A e B sono i due lati noti, e
· θ (theta) è l'angolo tra di loro.
A è indicato dalla linea viola nell'illustrazione a sinistra e B dalla linea arancione. C (in rosso) è il terzo lato, quello che calcoli.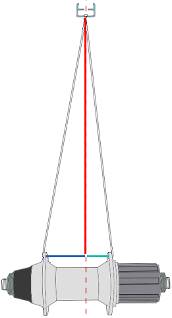
I due lati noti (A e B) sono il raggio (mezzo diametro) del cerchio dei fori dei raggi nella flangia del mozzo e il raggio del cerchio dei fori dei raggi del cerchio. L'angolo θ dipende dal numero di fori dei raggi e dallo schema di raggiatura.
Il primo passaggio crea un punto di misurazione virtuale direttamente sotto i fori dei raggi nel cerchio. Non c'è niente da misurare direttamente lì, ed è per questo che è necessario un secondo passaggio.
Il secondo passaggio fornisce la lunghezza del raggio, tenendo conto della distanza della flangia del mozzo dalla linea centrale. Questo passaggio applica il teorema di Pitagora per l'ipotenusa (lato obliquo) di un triangolo rettangolo, con una leggera correzione per tenere conto delle dimensioni dei fori dei raggi nel mozzo:
L u003d\/ C2 + w2 - d/2
dove:
· C è il risultato della formula precedente, come mostrato dalla linea rossa nell'immagine a destra,
· w è la spaziatura della flangia raggiante dalla linea centrale, come mostrato dalla linea blu o verde nell'immagine, e
· d è il diametro dei fori dei raggi nel mozzo.
Ciascuna delle due flange dell'hub può essere a una distanza diversa dalla linea centrale, come indicato dalle linee blu e verdi -- immagine modificata da una da keithonearth su Wikipedia.
Scrivi da: Sheldon Brown

 X
X